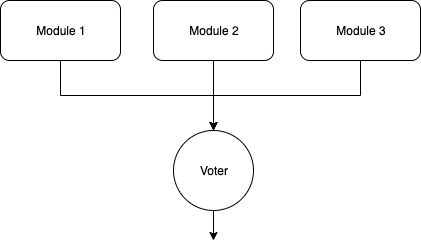
Triple Modular Redundancy (TMR) is a fault-tolerant technique, and it is a form of N-MR. In this method, computations are being done in three simultaneous flows, and in the end, a voter checks the results and chooses the most frequent one between the three outcomes (Fig.1). This scheme will help to cover unwanted faults. There are more to read on: Triple modular redundancy - Wikipedia
The purpose of this program is applying the TMR technique on conventional matrix multiplication. Three threads do matrix multiplication, and a voter chooses the majority as the best result. The code will run on both Windows and Linux systems, but the actual behavior may vary.
The code is split using predefined compiler macros in two parts, Linux and Windows. Windows version implemented using C++ standard thread library. The major problem with the thread library is that it is not possible to pin an individual thread to a specific CPU core. However, in Linux implementation, the core library is POSIX threads (pthread) that there is a possibility to define the desired affinity mask to assign a thread to a particular core of CPU. Read more on pthread: POSIX Threads - Wikipedia
On a Linux machine, the command g++ -O3 -pthread -std=c++11 Source.cpp -o TMP compiles and ./TMR runs the code. Following running the program, a menu will come up with the following options.
- Exit
- Hardware Concurrency Info. of Machine
- Input Matrices
- Generate Random Matrices with Pre-Defined Maximum Dimension (10x10)
- Show First Matrix
- Show Second Matrix
- Matrix Multiplication
- Show Multiplication Result
- Fault Simulation
- Dump Matrices to File
Putting self-explanatory options aside, number 1 shows maximum threads available on the machine using the standard C++ thread library. Option 8, simulates situations that each thread may face a fault. In theory, the chance of encountering a fault is nearly zero. Therefore, adding some intentional faults is helpful to observe the functionality of this technique.
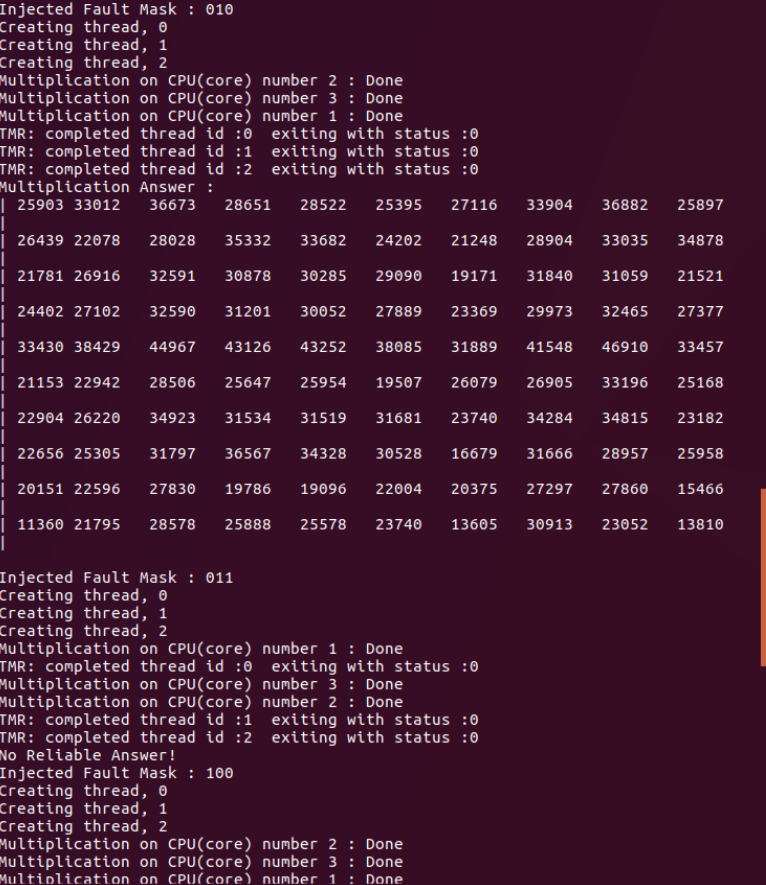 Fig.2: Fault Simulation Fig.2: Fault Simulation |
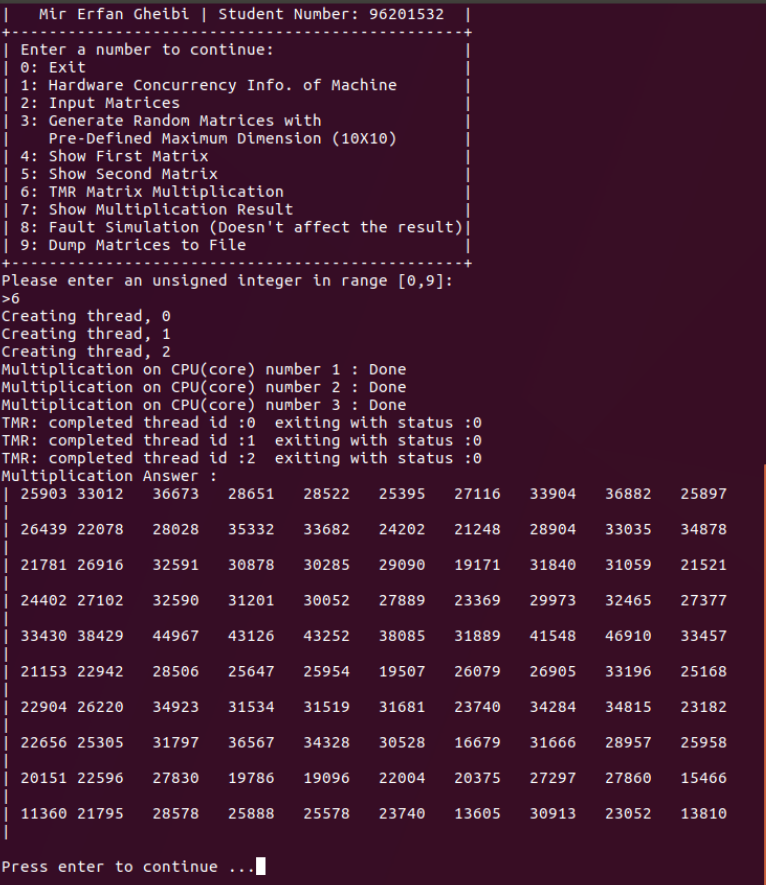 Fig.3: General Running Fig.3: General Running |
|---|
This program was a part of a take-home midterm exam of "Fault-Tolerant Systems Design" at Sharif University of Technology.