Natural neighbor interpolation is a method for interpolating scattered data (i.e. you know the values of a function at scattered locations). It is often superior to linear barycentric interpolation, which is a commonly used method of interpolation provided by Scipy's griddata function.
There are several implementations of 2D natural neighbor interpolation in Python. We needed a fast 3D implementation that could run without a GPU, so we wrote an implementation of Discrete Sibson Interpolation (a version of natural neighbor interpolation that is fast but introduces slight errors as compared to "geometric" natural neighbor interpolation).
See https://doi.org/10.1109/TVCG.2006.27 for details.
pip install naturalneighbor- Python 3.5+
- Numpy (has been tested with 1.13+)
Natural neighbor interpolation can be more accurate than linear barycentric interpolation (Scipy's default) for smoothly varying functions.
Also, the final result looks better.
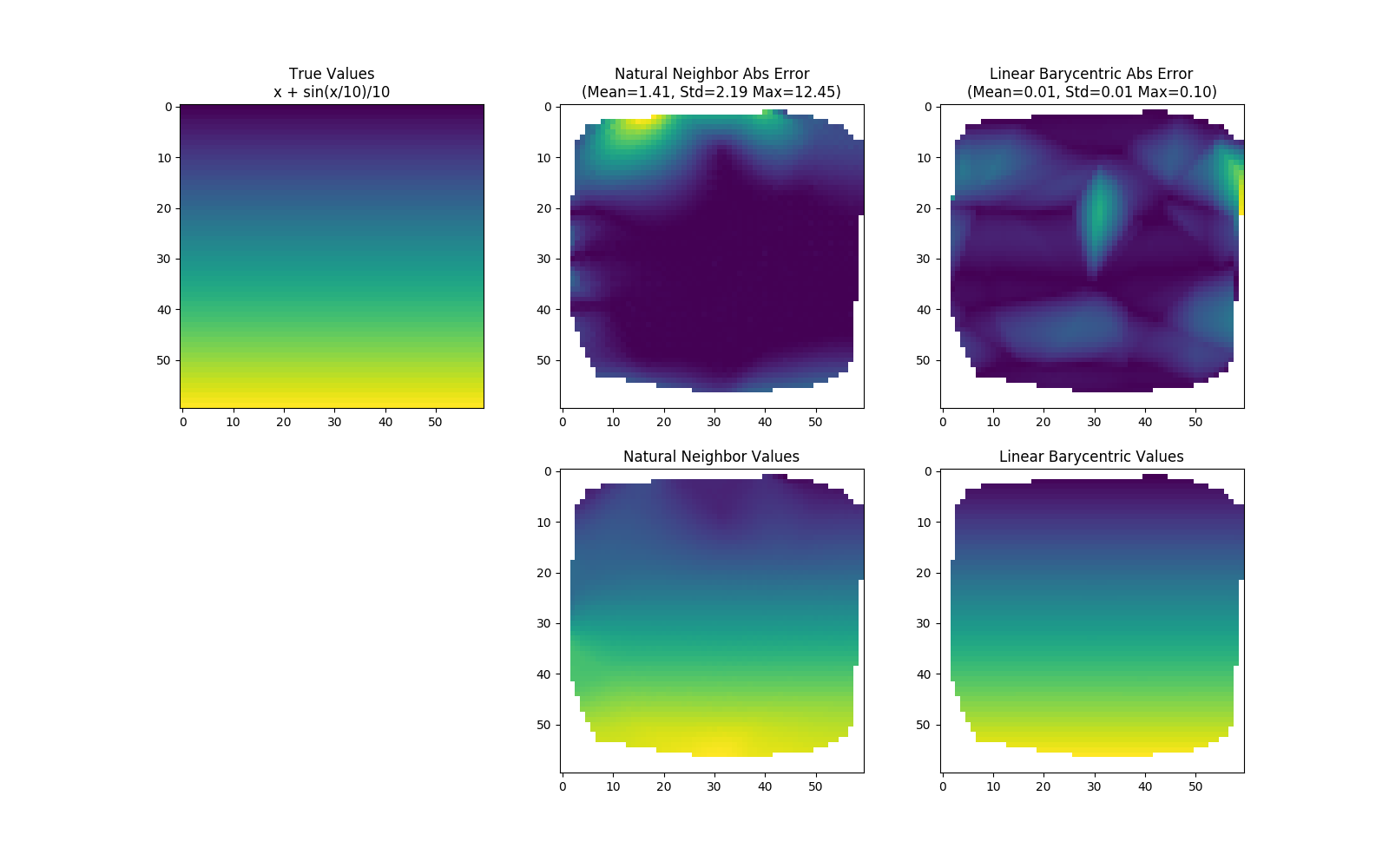
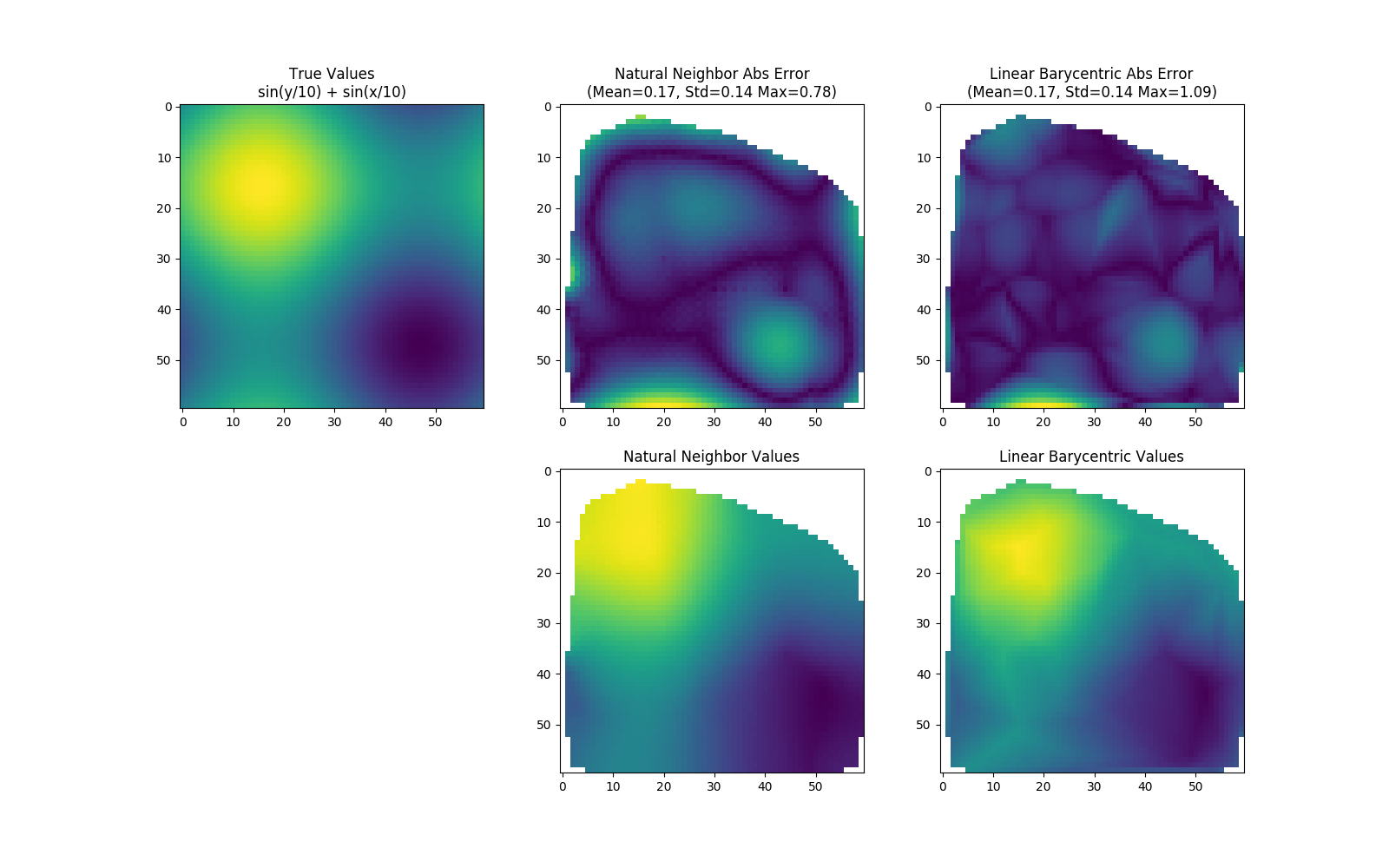
Note that the natural neighbor values usually are extrapolated; they were cut off in the demo to fairly compare with Scipy's linear barycentric method, which does not extrapolate.
This module exposes a single function, griddata.
The API for naturalneighbor.griddata is similar to
scipy.interpolate.griddata. Unlike Scipy, the third argument is not a
dense mgrid, but instead is just the ranges that would have been passed to mgrid. This is because the discrete Sibson approach requires the interpolated points to lie on an evenly spaced grid.
import scipy.interpolate
import numpy as np
import naturalneighbor
num_points = 10
num_dimensions = 3
points = np.random.rand(num_points, num_dimensions)
values = np.random.rand(num_points)
grids = tuple(np.mgrid[0:100:1, 0:50:100j, 0:100:2])
scipy_interpolated_values = scipy.interpolate.griddata(points, values, grids)
grid_ranges = [[0, 100, 1], [0, 50, 100j], [0, 100, 2]]
nn_interpolated_values = naturalneighbor.griddata(points, values, grid_ranges)- Provide options for extrapolation handling
- Support floats and complex numbers (only support doubles at the moment)
- Support 2D (only support 3D)
- Add documentation with discussion on limitations of discrete sibson's method
- Uncomment cpplint from tox.ini and cleanup C++ code
- Generalize the threading model (currently it uses 8 threads---one for each quadrant)