2304

2304. Minimum Path Cost in a Grid (Medium)

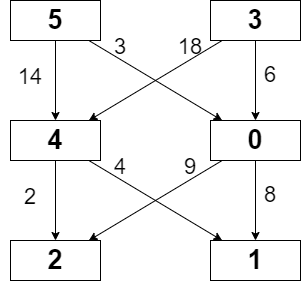
You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), ..., (x + 1, n - 1). Note that it is not possible to move from cells in the last row.

Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.

The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.

 

Example 1:

Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.

Example 2:

Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• grid consists of distinct integers from 0 to m * n - 1.
• moveCost.length == m * n
• moveCost[i].length == n
• 1 <= moveCost[i][j] <= 100

Companies: Google

Related Topics:
Array, Dynamic Programming, Matrix

Similar Questions:

• Unique Paths (Medium)
• Unique Paths II (Medium)
• Minimum Path Sum (Medium)
• Dungeon Game (Hard)
• Paint House (Medium)

Solution 1. DP

// OJ: https://leetcode.com/problems/minimum-path-cost-in-a-grid
// Author: github.com/lzl124631x
// Time: O(MN^2)
// Space: O(MN)
class Solution {
public:
    int minPathCost(vector<vector<int>>& A, vector<vector<int>>& C) {
        int M = A.size(), N = A[0].size(), ans = INT_MAX;
        vector<vector<int>> dp(M, vector<int>(N, INT_MAX));
        for (int j = 0; j < N; ++j) dp[M - 1][j] = A[M - 1][j];
        for (int i = M - 2; i >= 0; --i) {
            for (int j = 0; j < N; ++j) {
                for (int k = 0; k < N; ++k) {
                    dp[i][j] = min(dp[i][j], dp[i + 1][k] + A[i][j] + C[A[i][j]][k]);
                }
                if (i == 0) ans = min(ans, dp[i][j]);
            }
        }
        return ans;
    }
};

Solution 2. DP with Space Optimization

// OJ: https://leetcode.com/problems/minimum-path-cost-in-a-grid
// Author: github.com/lzl124631x
// Time: O(MN^2)
// Space: O(N) if we are not allowed to compute values in-place
class Solution {
public:
    int minPathCost(vector<vector<int>>& A, vector<vector<int>>& C) {
        int M = A.size(), N = A[0].size(), ans = INT_MAX;
        for (int i = M - 2; i >= 0; --i) {
            for (int j = 0; j < N; ++j) {
                int mn = INT_MAX;
                for (int k = 0; k < N; ++k) {
                    mn = min(mn, A[i + 1][k] + C[A[i][j]][k]);
                }
                A[i][j] += mn;
                if (i == 0) ans = min(ans, A[i][j]);
            }
        }
        return ans;
    }
};