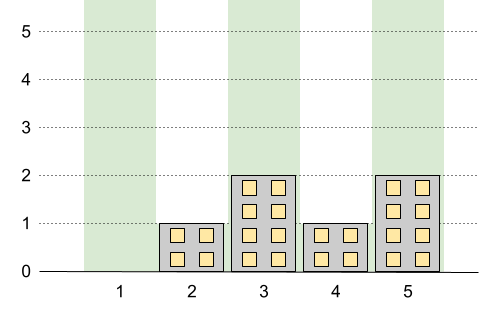1840. Maximum Building Height

1840. Maximum Building Height (Hard)

You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.

However, there are city restrictions on the heights of the new buildings:

• The height of each building must be a non-negative integer.
• The height of the first building must be 0.
• The height difference between any two adjacent buildings cannot exceed 1.

Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [idi, maxHeighti] indicates that building idi must have a height less than or equal to maxHeighti.

It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.

Return the maximum possible height of the tallest building.

 

Example 1:

Input: n = 5, restrictions = [[2,1],[4,1]]
Output: 2
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.

Example 2:

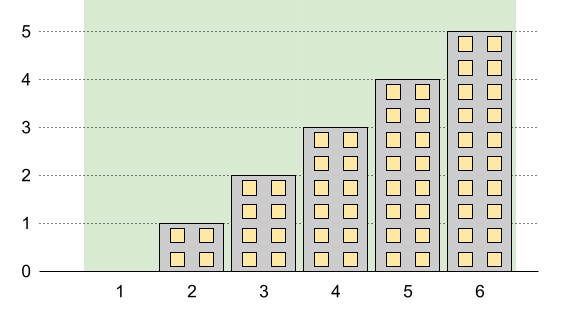
Input: n = 6, restrictions = []
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.

Example 3:

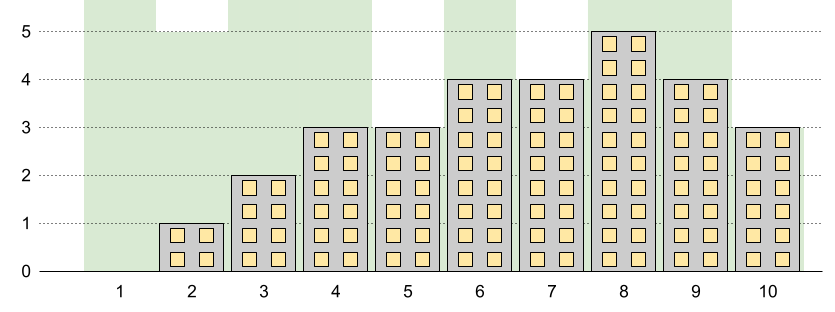
Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]
Output: 5
Explanation: The green area in the image indicates the maximum allowed height for each building.
We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.

 

Constraints:

• 2 <= n <= 109
• 0 <= restrictions.length <= min(n - 1, 105)
• 2 <= idi <= n
• idi is unique.
• 0 <= maxHeighti <= 109

Related Topics:
Binary Search, Greedy

Solution 1. Filter Critical Restrictions

We should remove the useless restrictions and only keep the critical ones.

Step 1. Remove Useless Restrictions

Put all the restrictions into a m which is a map from the x value to the height restriction. Note that m[1] = 0 should also be added.

Scan from left to right, assume two consecutive restrictions are a = [x1, h1] and b = [x2, h2] (x1 < x2). If h2 >= h1 + x2 - x1, b is useless and should be removed.

Scan from right to left, assume two consecutive restrictions are a = [x1, h1] and b = [x2, h2] (x1 < x2). If h1 >= h2 + x2 - x1, a is useless and should be removed.

Step 2. Calculate the max heights we can get between two consecutive restrictions

For two consecutive restrictions are a = [x1, h1] and b = [x2, h2] (x1 < x2), assume the tallest building between them is at position x, then one of the following is is true:

• When there is only one tallest building, h1 + x - x1 == h2 + x2 - x, so 2 * x = h2 - h1 + x1 + x2
• When there are two tallest buildings, h1 + x - x1 == h2 + x2 - x - 1, so 2 * x = h2 - h1 + x1 + x2 - 1.

So x = ceil( (h2 - h1 + x1 + x2) / 2 ), and the corresponding height is h1 + x - x1.

One special case is the last restriction [x, h]. The height we can get using it is h + n - x.

// OJ: https://leetcode.com/problems/maximum-building-height/
// Author: github.com/lzl124631x
// Time: O(RlogR)
// Space: O(R)
class Solution {
public:
    int maxBuilding(int n, vector<vector<int>>& A) {
        map<long, long> m{{1,0}};
        for (auto &v : A) m[v[0]] = v[1];
        long ans = 0;
        for (auto it = next(begin(m)); it != end(m);) {
            auto [x1, h1] = *prev(it);
            auto [x2, h2] = *it;
            if (h2 >= h1 + x2 - x1) {
                it = m.erase(it);
            } else {
                it = next(it);
            }
        }
        for (auto it = prev(end(m)); it != begin(m);) {
            auto [x1, h1] = *prev(it);
            auto [x2, h2] = *it;
            if (h1 >= h2 + x2 - x1) {
                m.erase(prev(it));
            } else {
                it = prev(it);
            }
        }
        for (auto it = next(begin(m)); it != end(m); ++it) {
            auto [x1, h1] = *prev(it);
            auto [x2, h2] = *it;
            long x = (h2 - h1 + x1 + x2) / 2;
            ans = max(ans, h1 + x - x1);
        }
        auto [x, h] = *rbegin(m);
        ans = max(ans, h + n - x);
        return ans;
    }
};

Solution 2.

// OJ: https://leetcode.com/problems/maximum-building-height/
// Author: github.com/lzl124631x
// Time: O(RlogR)
// Space: O(1)
// Ref: https://leetcode.com/problems/maximum-building-height/discuss/1175047/PythonC%2B%2B-greedy-solution-with-visual-explanation-O(MlogM)
class Solution {
public:
    int maxBuilding(int n, vector<vector<int>>& A) {
        A.push_back({1, 0});
        sort(begin(A), end(A));
        int N = A.size(), ans = 0;
        for (int i = 1; i < N; ++i) {
            int x1 = A[i - 1][0], h1 = A[i - 1][1];
            int x2 = A[i][0], &h2 = A[i][1];
            h2 = min(h2, h1 + x2 - x1);
        }
        for (int i = N - 2; i >= 0; --i) {
            int x1 = A[i][0], &h1 = A[i][1];
            int x2 = A[i + 1][0], h2 = A[i + 1][1];
            h1 = min(h1, h2 + x2 - x1);
            int mid = (h2 - h1 + x1 + x2) / 2;
            ans = max(ans, h1 + mid - x1);
        }
        return max(ans, A.back()[1] + n - A.back()[0]);
    }
};