|
| 1 | +--- |
| 2 | +title: How to train a good model 1 |
| 3 | +date: 2023-07-11 16:50 |
| 4 | +tags: |
| 5 | +decsription: |
| 6 | +cover: https://api.r10086.com/%E6%A8%B1%E9%81%93%E9%9A%8F%E6%9C%BA%E5%9B%BE%E7%89%87api%E6%8E%A5%E5%8F%A3.php?%E5%9B%BE%E7%89%87%E7%B3%BB%E5%88%97=%E5%8A%A8%E6%BC%AB%E7%BB%BC%E5%90%882 |
| 7 | +--- |
| 8 | + |
| 9 | + |
| 10 | +# How to train a good model |
| 11 | + |
| 12 | + |
| 13 | +## A good setup |
| 14 | + |
| 15 | +To train a good model, apart from designing an overall model structure, we should prepare suitable training components for our training to get the model converge. They includes: |
| 16 | + |
| 17 | +- Activation functions |
| 18 | + |
| 19 | + Use ReLU for the first hand, may be good enough |
| 20 | + |
| 21 | +- data preprocessing |
| 22 | + |
| 23 | + Depending on the tasks, different Conv Nets structure use different data preprocessing techniques. |
| 24 | + |
| 25 | +  |
| 26 | + |
| 27 | + |
| 28 | + |
| 29 | +- weight initialization (Kaiming & Xavier initialization) |
| 30 | + |
| 31 | + We can initialize the weight according to gaussian distribution with mean 0 and arbitrary standard deviation. But it turns out that bigger or smaller `std` will all hamper the convergence of the model. |
| 32 | + |
| 33 | + **Kaiming and Xavier initialization** deals with the initialization problem. Specifically, Kaiming method is an extension of Xavier's with respect to ReLU activation circumstances. |
| 34 | + |
| 35 | + The formular of Kaiming & Xavier initialization should be: |
| 36 | + $$ |
| 37 | + \sigma = \sqrt{\frac{k}{D_{in}}} \space |
| 38 | + $$ |
| 39 | + In the above formular, |
| 40 | + |
| 41 | + - $\sigma$ is the standard deviation over this batch of data |
| 42 | + |
| 43 | + - k = 2 if the layer in which lays our weight matrix to be initialized contains a ReLU function, which is the Kaiming method. And k=1 if not ReLU, is the Xavier method. |
| 44 | + |
| 45 | + - **$D_{in}$ is the number of the inputs that is sent to a single neuron / kernel and spit out a single output.** For example, for FC layer, $D_{in}$ is the dimension of a single sample, for convolution layer, $D{in}$ is `feature_number * kernel_size * kernal_size` . The common points is that they are all sent to a column of W or a kernel and output a single scalar in the output matrix. |
| 46 | + |
| 47 | + > The derivation of the method is about keeping the variance of output = variance of input in a layer. Detained steps please refer to [cs231 notes](https://cs231n.github.io/neural-networks-2). |
| 48 | +
|
| 49 | +- regularization( broadly include *Dropouts* and *Batch Normalizations*) |
| 50 | + |
| 51 | + **L2** and **L1-norm** regularization are common in shallow network architecture. |
| 52 | + |
| 53 | + Other methods including Elastic net regularization and Max-norm regularization` are available but not used often. |
| 54 | + |
| 55 | + **Dropout** is another very useful and once popular method of regularization. Dropout claims to improve robustness by randomly dropout some neurons, which prevents overfitting by inhibiting feature co-expression on nodes (overmixing distinctive and informative features). |
| 56 | + Others see dropout as a result of ensembled learning on subnetworks from the whole network. However global pooling layers have take the place of dropout in large neural networks in recent works. |
| 57 | + |
| 58 | + **Batch Normalization** is another widely used method in Deep network model. One way of interpreting BN is its regularization property. Because BN normalize the data for each feature, across all the samples in a batch. This is similar to what L1 & L2 norm do to the loss function & data in a batch. But also Batch Normalization can be interpreted as a way of online/in-model data 'pre' processing. It did similar job to data preprocessing, but is integrated in the model training and requires updates on its only parameters using front/backpropagation. The details of batch normalization can be see in this [class video](https://www.bilibili.com/video/BV13P4y1t7gM?p=7&vd_source=1322e7434ed7c2f65007f763fffec246) |
| 59 | + |
| 60 | +To clarify, these are not the hyperparameters in model training, but more sort of options that may change the whole model structure. |
| 61 | + |
| 62 | +Choosing the right spare parts is the first step of training a good model. But online tuning is also crucial for a network model to converge. |
| 63 | + |
| 64 | +## Training techniques |
| 65 | + |
| 66 | +There are several process that we need to follow to train a good model by hand. |
| 67 | + |
| 68 | +### Sanity checks |
| 69 | + |
| 70 | +Sanity checks deals with the implementation errors in the model design. We can check **loss** and **gradient** by running one round of `model.loss(X_train, y_train=None)` . |
| 71 | + |
| 72 | +- Loss checking |
| 73 | + By a single computation, the loss function value should be closely relative to the loss function and weight initialization, not the data distribution. For example, in `softmax` we expect loss = $\log C$ for $C$ class supervised classification learning. |
| 74 | +- Gradient checking |
| 75 | + We can use numeric gradient checking to assure the correctness in backprop. We should use artificial data in small scale and running one round of `model.loss(X_train,y_train)` . We expect a close value between the numerical result and the analytical results. |
| 76 | +- Overfit a small data set |
| 77 | + Tune the parameter on a small training set that achieve 100% accuracy (likely getting low validation accuracy). For example, take 100 samples, use 30 epochs, within each epoch, use SGD to fetch a batch_size of 50 samples (accounts for 100//50 = 2 iterations per epoch). |
| 78 | + |
| 79 | +For details please refer to the [class notes](https://cs231n.github.io/neural-networks-3/) |
| 80 | + |
| 81 | + |
| 82 | + |
| 83 | +### Watching the Dashboards |
| 84 | + |
| 85 | +- Accuracy on training and validation |
| 86 | + |
| 87 | + 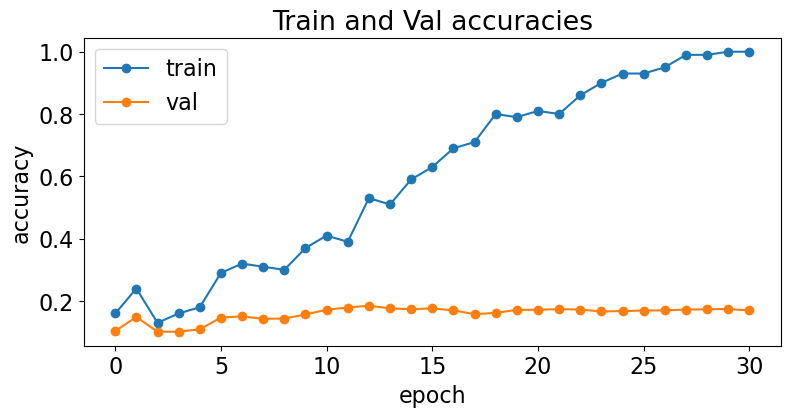 |
| 88 | + |
| 89 | +- Loss value |
| 90 | + |
| 91 | + 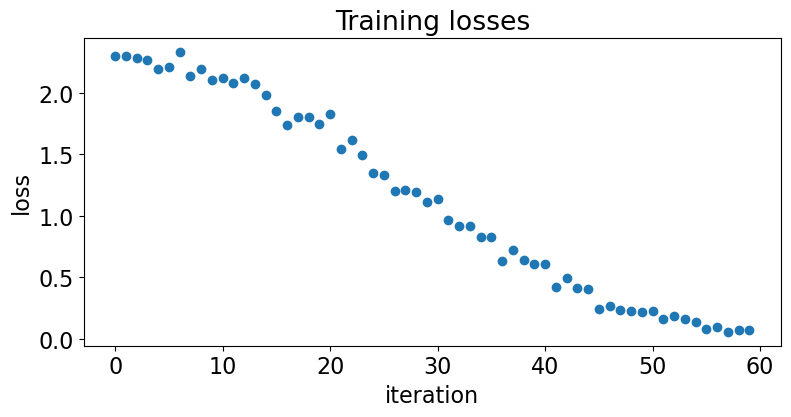 |
| 92 | + |
| 93 | +These are the two important indicators of training, make sure to look at the two picture in tuning. |
| 94 | + |
| 95 | +### Update rules |
| 96 | + |
| 97 | +Several GD rules have been developed these years. In default we can use the Adam method. |
| 98 | + |
| 99 | + |
| 100 | +### Hyperparameters tuning |
| 101 | + |
| 102 | +There are **two common source of hyperparams** in network training. |
| 103 | + |
| 104 | + The first is from the configuration params of model components, like `hidden_layers`, `num_filters` , `regularization_strength` and so on. They are related more closely to the performance of the model. |
| 105 | + |
| 106 | +The second is from the solver's params, like `learning_rates` , `update_rules` and so on. They are related more closely to the convergence of the model. |
| 107 | + |
| 108 | + Among them, **Learning rates and its decays** are utmost important for most training tasks. |
| 109 | + |
| 110 | +Before we use random search, we should **first pinpoint a suitable range for our search**. We can use method of **Overfitting small data** |
| 111 | + |
| 112 | +**Then, try to optimize the learning rate, lr_decay and regularization strength first.** |
| 113 | + |
| 114 | +**Finally, tune other parameters to the best effort.** |
| 115 | + |
| 116 | +Several notice: |
| 117 | + |
| 118 | +- Use one large validation set is enough |
| 119 | + |
| 120 | +- Use random search |
| 121 | + |
| 122 | + Further, if the best value is on the edge of the range, try again with modified range |
| 123 | + |
| 124 | +- From coarse to fine |
| 125 | + |
| 126 | + At first, do broad range search with relatively small number of epochs. After that, narrow down to a more optimized range and increase epochs. |
| 127 | + |
| 128 | +For example, a training code may look like this: |
| 129 | + |
| 130 | +```python |
| 131 | +#... |
| 132 | + |
| 133 | +# parameters here are about the structure of the model, not hyperparameters usually, but we can also investigate on them |
| 134 | +for a in search_range_a: |
| 135 | + for b in search_range_b: |
| 136 | +#... |
| 137 | + |
| 138 | + model = ThreeLayerConvNet(num_filters=3, filter_size=3, |
| 139 | + input_dims=input_dims, hidden_dim=7, |
| 140 | + weight_scale=5e-2, dtype=torch.float64, device='cuda') |
| 141 | + |
| 142 | +# These are hyperparameters for solving the model, |
| 143 | + solver = Solver(model, data_dict, |
| 144 | + num_epochs=1, batch_size=64, |
| 145 | + update_rule=adam, |
| 146 | + optim_config={ |
| 147 | + 'learning_rate': 2e-3, |
| 148 | + }, |
| 149 | + verbose=True, print_every=50, device='cuda') |
| 150 | + solver.train() |
| 151 | + |
| 152 | +``` |
| 153 | + |
| 154 | + |
| 155 | + |
| 156 | +## Afterward training |
| 157 | + |
| 158 | +TBD |
0 commit comments